建议先阅读之前两篇文章:
0. 写在前面
在上一篇介绍的神经网络语言模型中,我们训练模型的目标是得到一个泛化能力强、无需平滑的语言模型,而词向量只是我们在训练语言模型过程中的一个副产物,这个副产物可以起到词嵌入的作用,将语料库中的词语映射为一个个的向量,且向量能够表征一定的语义信息。那么,从词嵌入的角度出发,我们是否可以使用这个模型专门用于将词语转换为向量呢?可以当然是可以,不过有以下问题需要考虑:
- 语言模型由于其任务限制,只能使用前面的词语来预测当前词,缺少后面词语的上下文信息。
- 模型的最后一层softmax层计算非常耗时。
因此,如果要使用神经网络来实现词嵌入,我们需要对神经网络语言模型进行一定的改进。接下来,就让我们看看Word2Vec是如何解决以上问题的。
PS. 关于Word2Vec的代码和数学推导,网上以及文末的参考资料中都要非常好且详细的介绍,这篇文章并不想重复前人工作,因此,本文在基本概念之外,也加入了许多理解性的东西(如对语义如何建模到向量中的理解,词向量维度的理解等),希望能够起到参考价值。
1. Word2Vec概览
Word2Vec并非指一个模型,而是2013年Google开源的一个获取词向量的工具包,由于简单高效,大大降低了词向量在工业界的应用门槛。我们先来看下Word2Vec能够取得的效果:
- 相似词:通过向量间距离的远近来寻找相似词,如man的相似词woman;
- 词语线性运算:V(King) - V(man) + V(woman) = V(Queen)
由此可见,Word2Vec可以通过上下文将语义较好的嵌入到向量空间中。由于Word2Vec生成的词向量将自然语言的特征较好地融合进了低维度稠密词向量中,使用词向量进行后续的各种NLP任务便可以取得较好的结果。
Word2Vec本身的模型结构是比较简单的,但模型结构以外有许多需要理解的内容,对Word2Vec的理解可以帮助我们更好地调节深度学习模型参数,更好地理解包括BERT在内的后续各个模型。要理解Word2Vec,我们主要需要了解其中的四个概念:
- CBOW
- Skip-gram
- Hierarchical softmax
- Negative Sampling
其中,前两个代表Word2Vec中两种不同的获取词向量的策略,或者说模型结构;后两个则是两种改进softmax计算复杂度过高问题的方法。
这篇文章将对以上四个概念进行深入剖析,之后将给出对Word2Vec如何建模语义信息的理解和对词向量维度的理解。
2. CBOW & Skip-gram
首先,与语言模型只使用当前词前面的词语不同,我们将使用当前词周围的词来建模词向量。其次,要明确的是,CBOW和Skip-gram都是使用浅层的神经网络,他们的区别在于输入和输出的不同。
CBOW:以当前词的周围词语作为输入,当前词作为输出。即上下文预测当前词。
Skip-gram:以当前词作为输入,当前词的周围词作为输出。即当前词预测上下文。
2.1 CBOW
CBOW使用当前词周围的词语来预测当前词,所谓周围词,既包括前面的词语,也包括后面的词语。至于取前后几个词语,由Context window指定。
还是举例子🌰来说明:
我们有一个句子:“知识改变命运”。分词为[“知识”, “改变”, “命运”]。构造词表为{0:
使用CBOW的方法,取Context window=1,构造样本为:
, 改变 —> 知识 知识,命运 —> 改变
改变,
—> 命运
接下来,和神经网络语言模型一样,我们为词表中的每个词语分配一个随机初始化的词向量(瞎编的数字😁):
其中,矩阵的第一行为词表中序号为0的词语的词向量,以此类推。注意,我们最终的目标并不是得到一个神经网络模型,而是得到更新后的词向量矩阵。
为了方便起见,我们先从一个上下文词语预测当前词开始,比如使用「知识」这个词去预测「改变」。神经网络的输入为知识这个词的词向量,输出为预测词表中的所有词出现的概率。目标是最大化「改变」这个词出现的概率,即P(改变|知识)。其结构如下图所示(画功拙劣,凑活着看吧~👀):
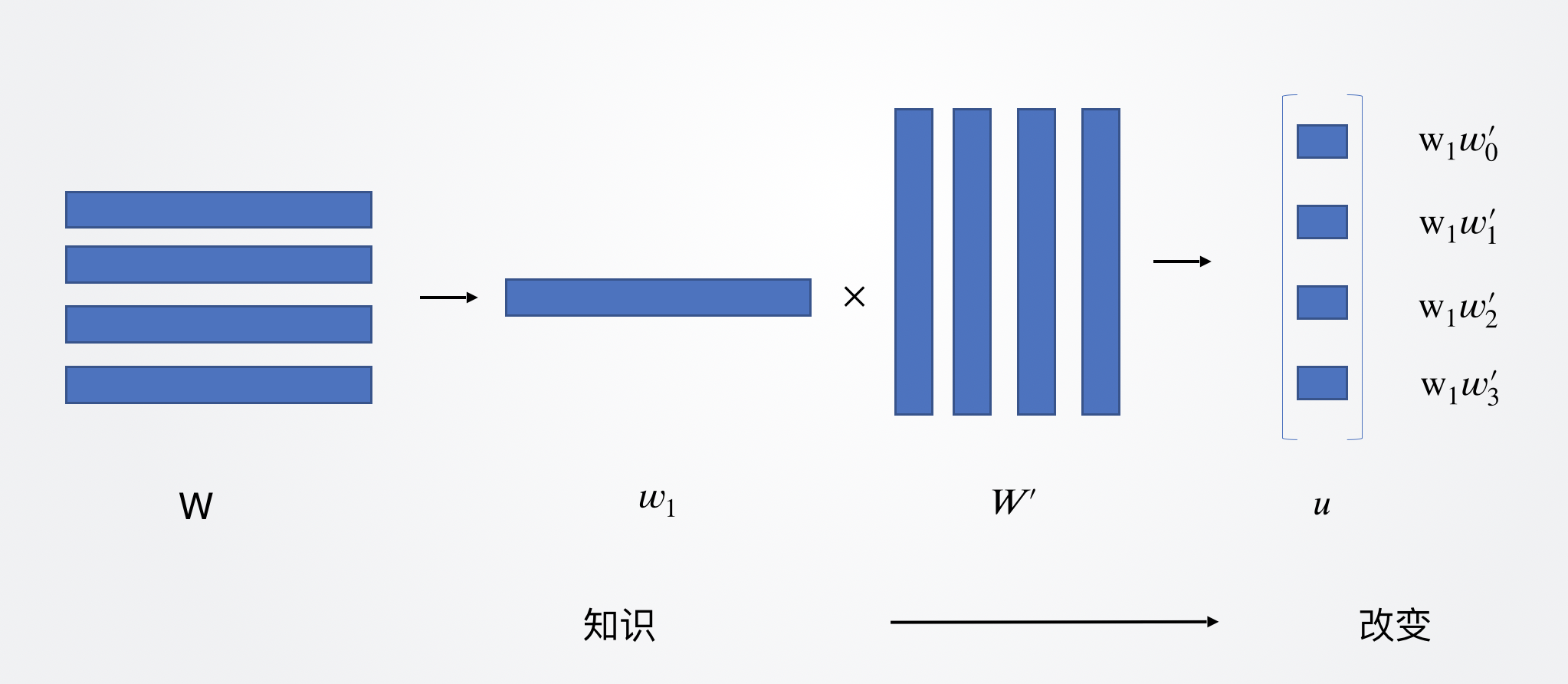
这里其实就是一个单层的全连接层神经网络,不过我没有按普通的神经网络那样画(画成这样是由于后面需要~)。由于一层全连接神经网络其实就是一次矩阵运算,所以我这里画成了向量与矩阵的运算形式。W就是前面初始化的词向量矩阵,W到$w_1$这里,是「取」知识这个词的词向量的过程;W’是神经网络的权重矩阵,我这里画成了四个列向量(其实这四个列向量也可以看作是四个词语的词向量,W叫输入词向量,W’叫做输出词向量。一般使用输入词向量。);最后的结果是$w_1$与四个列向量做内积得到的值组成的输出向量。
最后的输出向量做一次softmax运算,就可以得到词表中四个词语的概率了。然后针对损失函数使用反向传播进行优化就行了。
需要注意的是,在这个神经网络的训练过程中,需要更新的参数不只是其权重矩阵W’,还有其输入$w_1$。
再来看「知识」和「命运」预测「改变」的情况,结构图如下:
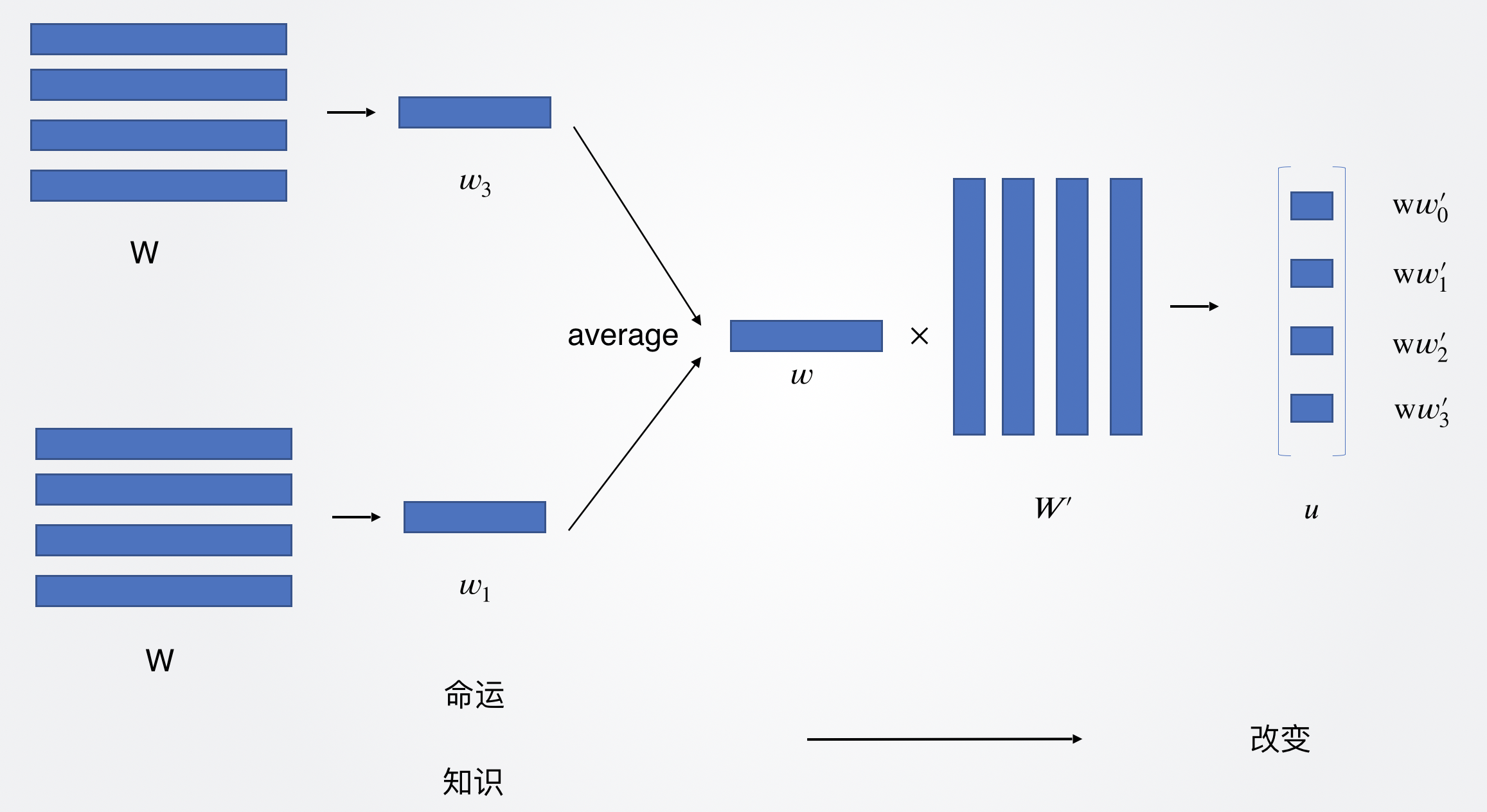
和上面那张图的差异在于输入。当两个上下文词语预测当前词时,神经网络的输入为「知识」和「命运」这两个词语的词向量的平均。之后的过程就一样了。注意,使用这个样本训练过程中,更新的参数为神经网络的权重矩阵W’和两个词向量$w_1$和$w_3$。
以上就是CBOW得到词向量的策略了,主要就是利用单层神经网络使用上下文预测当前词。
有了以上基础,再看Skip-gram就简单明了了。
2.2 Skip-gram
skip-gram以当前词作为输入,当前词的上下文词语作为输出。这个策略在构造样本时有两个概念需要清楚,一个是skip_window,类似于CBOW的context_window,用于指定选取上下文时的单侧窗口大小;另一个是num_skips,表示我们将从上下文窗口中选取几个词作为label。
同样还是「知识改变命运」这个例子,以skip_window=1, num_skips=2构造以下样本(这里我没有构造填充词):
改变—> 知识
改变—>命运
有了输入和输出,接下来的训练方式就是正常的神经网络的训练了。
实际实现过程中,有一些需要注意的点。
以上面例子为例,构造样本时,若num_skips=1,我们需要在窗口的两个词中取一个作为label;取词的方式为随机取一个,这里的随机并不是等概率随机,而是词频越高概率越高。
上面的例子看起来是构造了两个样本,但在实际训练过程中,这两个样本共同组成一个样本用于计算损失函数:
从极大似然估计的角度来看,我们要最大化P(知识|改变)和P(命运|改变)的乘积。由于加了log,乘积的形式变成了相加的形式。这等价于两个子样本组成一个batch计算损失函数。如果你读过word2vec的源码的话,你会发现,skip-gram在构造样本时,并非是将CBOW中的([知识,命运],改变)翻转为(改变,[知识,命运]),而是构造了两个样本:(改变,知识),(改变,命运)。实际运算时,只需要将上述样本放在同一个batch里面就行了。这也是为什么代码里需要保证batch_size % num_skips == 0。
另外,关于CBOW和Skip-gram的表述,你可能看到比较多的是以下两幅图:
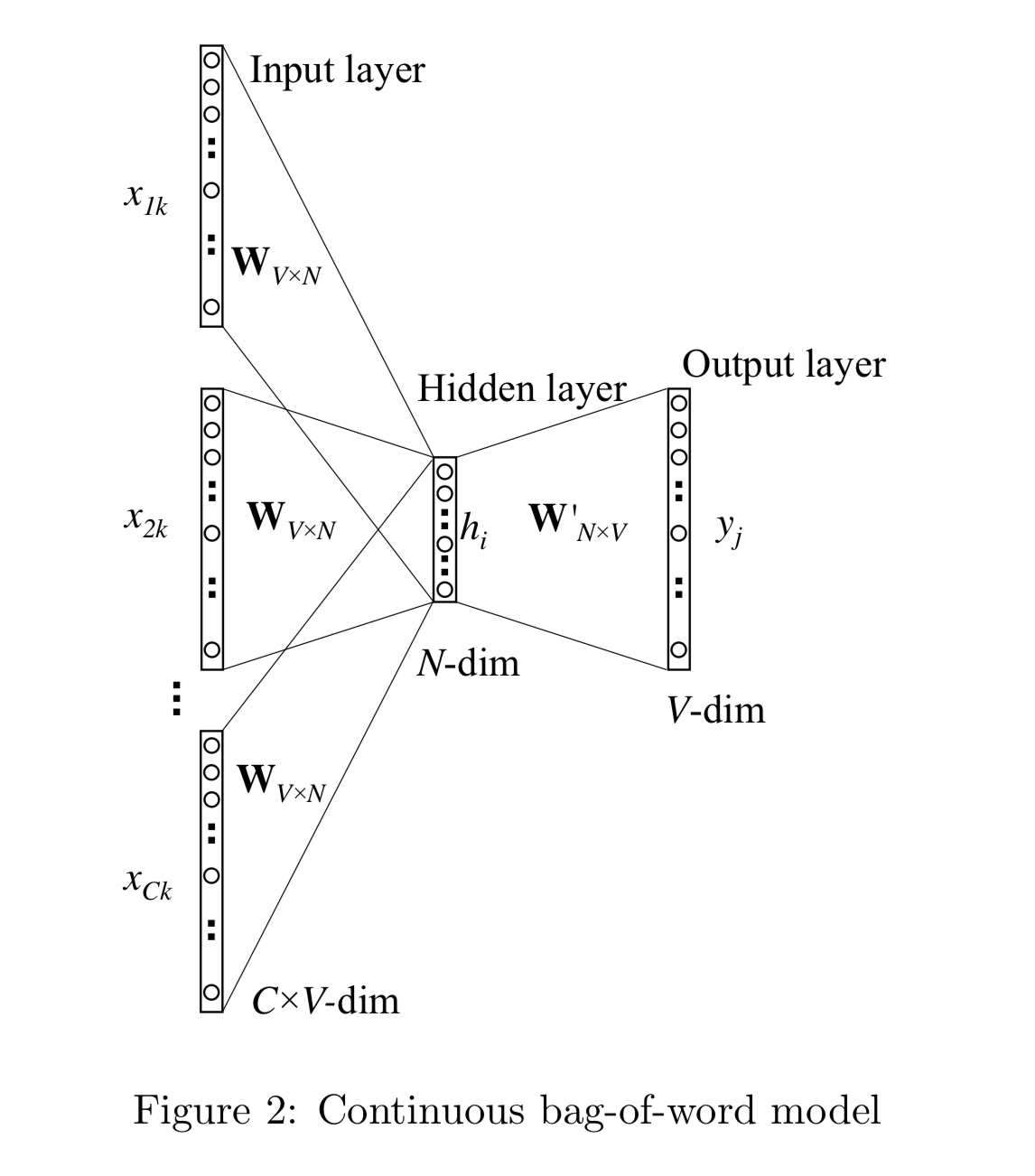
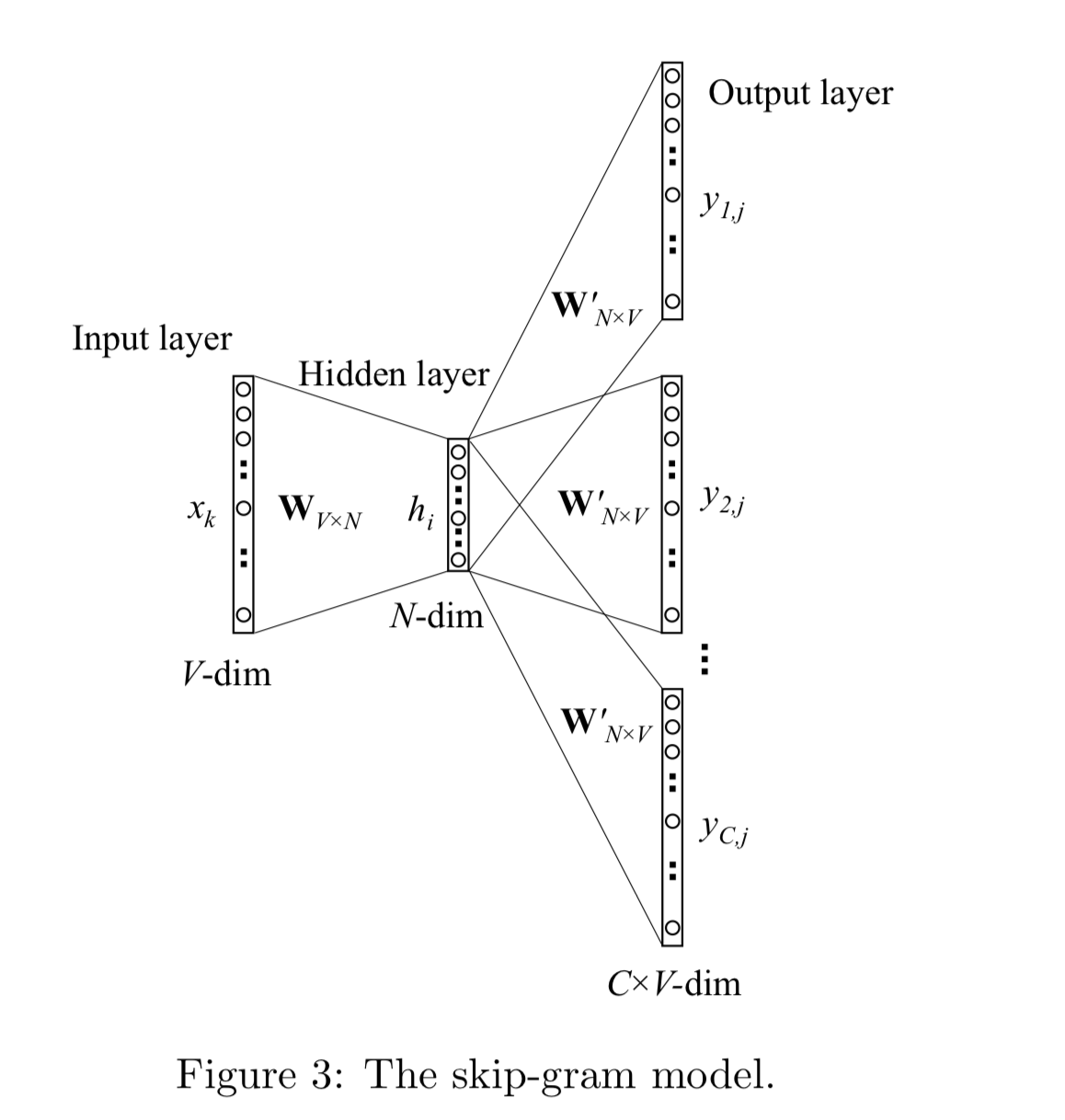
看起来比我前面画的神经网络多了一层,但其实是一样的。这两幅图将「取」词向量这一步作为了神经网络的第一层,使用词语的one-hot编码(即上图中的输入层)与词向量矩阵(即上图中第一层的权重矩阵)相乘,其实就是取词向量矩阵中,词语编号对应的那一行。
2.3 比较
根据Word2Vec作者Mikolov的说法,两者的比较如下:
Skip-gram: works well with small amount of the training data, represents well even rare words or phrases. CBOW: several times faster to train than the skip-gram, slightly better accuracy for the frequent words.
这里给出我对以上比较的理解。
关于训练集大小:Skip-gram在数据集较小时能取得更好的效果;原因我认为有两点:1. 数据集较小时,低频词较多,Skip-gram对低频词的表示效果较好(原因后面会说);2. 同样的语料库,Skip-gram能产生更多(子)样本。
关于训练速度:CBOW训练速度更快。这是因为,一个batch中,CBOW包含batch_size个中心词样本,Skip-gram包含batch_size/num_skips个中心词样本,同样的batch_size遍历一次样本集,CBOW需要更少的step。
关于低频高频词的表示效果:Skip-gram对低频词的表示效果优于CBOW,CBOW对高频词的表示效果略优于Skip-gram。原因的话,我从两个方面进行阐述:1. 直观上来理解,CBOW通过上下文预测中心词,如知识___命运,类似于完形填空,选择概率最高的一个词填入其中,这就要求词向量对于概率最高的那些词有足够的「理解」;而Skip-gram则是根据中心词填周围的词,如___改变___,要在中心词周围填词,词向量需要对该词有足够的「理解」才能填词,包括低频词。2. 从反向传播更新词向量的角度来看,在反向传播更新词向量时,CBOW使用相同的梯度更新所有输入词向量,如对于([知识,命运],改变)这个样本,知识和命运的词向量使用同样的梯度进行更新,这就使得低频词的词向量更新被高频词「平滑」掉了。而Skip-gram则不存在这个问题。
3. Trick
到了这里,其实就不属于模型结构介绍的范畴了,这一块主要是为了加速模型训练,使模型能够应用于大规模语料库。
首先看一下为什么softmax层这么费时。
softmax的公式如下:
可以看出,针对一个高维向量,即使要计算softmax后的一个元素值,也需要针对所有元素做指数运算,当维度非常高时,这种计算无疑是非常费时的。在word2vec中,需要做softmax运算的向量维度为词表词语个数,当语料库非常大时,词表词语个数也会变得非常大。但我们关注的只是某一个词的概率,即计算softmax后的某一个元素值,这里肯定存在许多无用计算。
3.1 Hierarchical softmax
分层softmax的出发点是,将词表中的所有词语组织成一棵哈夫曼树,计算词语出现概率时,使用从根节点到词语所在叶节点路径上的向量进行运算。这种方法不仅降低了softmax层的运算,还减少了输出层的计算量。
具体来说,先将词表中的词语组织到哈夫曼树的叶节点上。什么是哈夫曼树以及如何构建网上有很多资料,这里不再赘述了。简单来说,这里使用的哈夫曼树就是一棵二叉树,每个非叶节点存放一个向量(可以理解成神经网络中的参数,需要在训练过程中更新),每个叶节点存放一个词语,词语的词频越高,该叶节点离根节点越近。
还是以「知识 改变 命运」为例,使用「知识」预测「改变」,假定语料库中的词频知识>改变>命运,则模型简单结构和构建的哈夫曼树如下图:
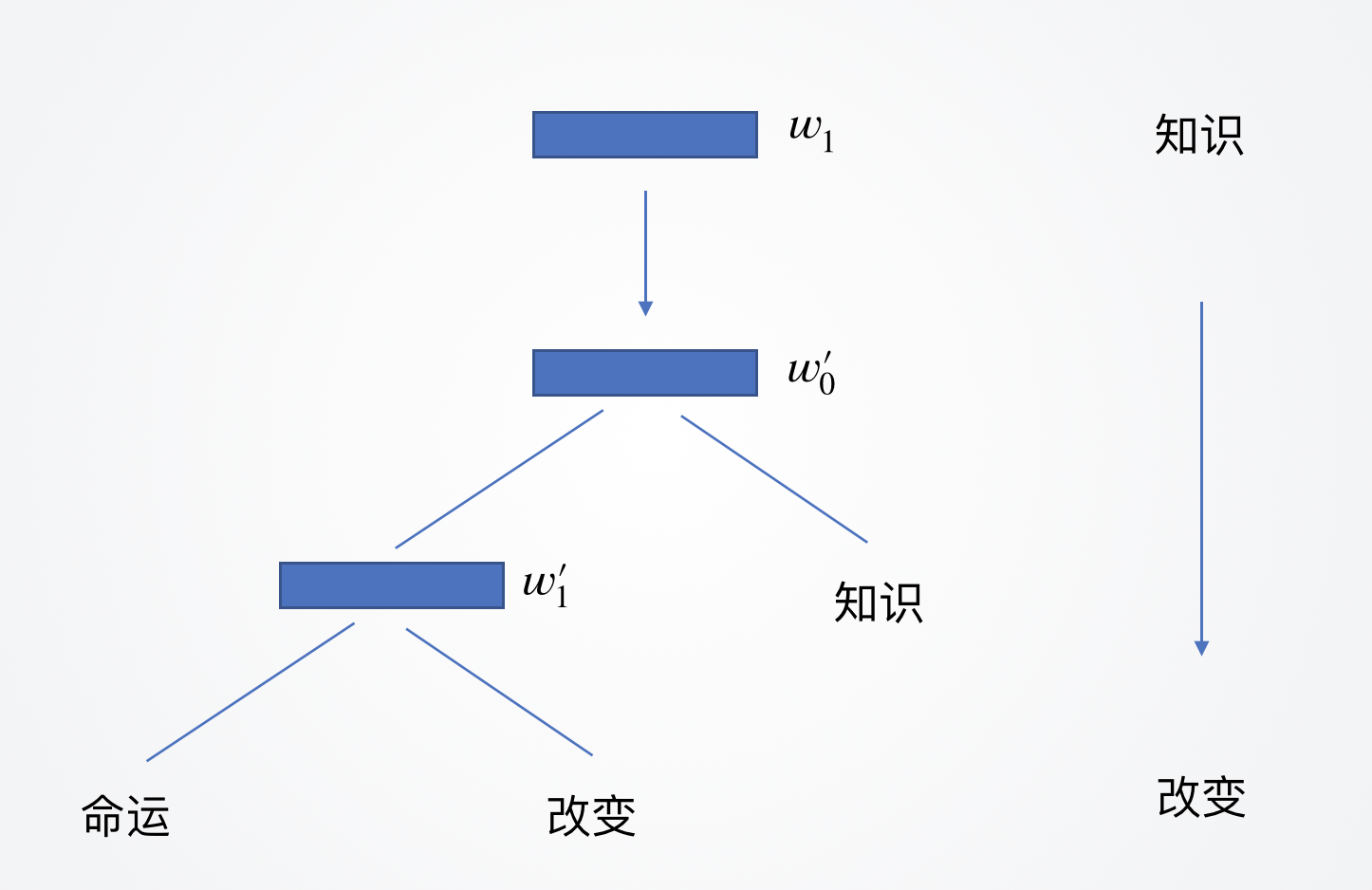
前面的步骤都一样,取知识的词向量 $w_1$,然后让我们随着词向量的脚步进入哈夫曼树,来看看如何得到P(改变|知识):
首先,$w_1$ 来到了根节点,碰到了向量$w^{‘}_0$ , 两个向量迫不及待地做了一次内积运算,得到一个值:$w_1w^{‘}_0$ 。接下来就面临道路的选择,走左边还是走右边?我们可以将这个问题看作一个二分类问题,规定走左子树为负类,右子树为正类,使用sigmoid函数来解决这个问题(类似于逻辑斯蒂回归):
因此,被分为正类的概率为$\sigma \left(w_1w^{‘}_0 \right)$ ,负类的概率为 $1-\sigma \left(w_1w^{‘}_0 \right)$ 。
要决定选择哪条路,得看我们的目标。这里的目标是抵达「改变」所在的叶节点,该叶节点在左子树上,因此需要走左边。到达左子树的「根节点」后,与前面一样,$w_1$ 又和该节点上的向量做了一次内积运算,不同的是,这次需要走右边来找到「改变」。因此:
有了目标函数,接下来根据链式求导法则就可以求出参数更新公式了。后续的具体推导可以参考资料【2】。
3.2 Negative Sampling
Negative Sampling(NEG)使用简单的随机负采样来代替复杂的哈夫曼树,大幅提高性能,可以作为Hierarchical softmax的一种替代方法。
同样以「知识 改变 命运」为例,使用「知识」预测「改变」,那么「改变」这个词就是一个「正样本」, 其他的所有词为「负样本」, 假设我们采集到的负样本集合为{命运},那么我们需要最大化:
其中$w^{‘}_2和w^{‘}_3$分别为「改变」和「知识」的输出词向量(即$W^{‘}$的第三列和第四列列向量)。
乘号前面表示预测为正样本的概率,后面表示预测不是负样本的概率。因此,最大化P可以理解为,增大预测正样本的概率同时降低预测负样本的概率。
另外,负样本的采集为随机采集,同样,这里的随机也并不是等概率随机,而是根据各个词语所占的词频比例进行相应概率的采样。
3.3 比较
由于Hierarchical Softmax使用了哈夫曼树,非叶节点的数量并不等于词语的数量,因此也没有了「输出词向量」这个概念,可能会损失一些效果(如Glove中,最后效果最好的词向量为输入词向量和输出词向量的平均)。
根据word2vec官网,两者的比较如下:
hierarchical softmax : better for infrequent words
negative sampling : better for frequent words, better with low dimensional vectors
4. 几点思考与理解
4.1 对语义建模的理解
Word2Vec主要是通过词语与其上下文之间的关系来对语义进行建模的。出发点就是拥有相同上下文的词语语义更加相似,体现到词向量上,就是拥有相同上下文的词语的词向量距离更近。如“苹果是一种水果”,“香蕉是一种水果”,苹果和香蕉拥有相同的上下文词语,那么我们认为苹果和香蕉的语义是相似的,它们的词向量的距离也应该是更近的。那么Word2Vec是怎么做到的呢?
要理解这一点,我们需要来简单地看一下反向传播的过程。针对图一:
计算softmax后的向量各元素值为:
损失函数为:
损失函数对输出层的梯度为:
损失函数对「知识」这个词的词向量的梯度为:
「知识」这个词的词向量的更新公式为:
以上,我们就推出了原始形式下,word2vec的词向量更新公式。让我们以图形的形式来理解一下这个更新公式:
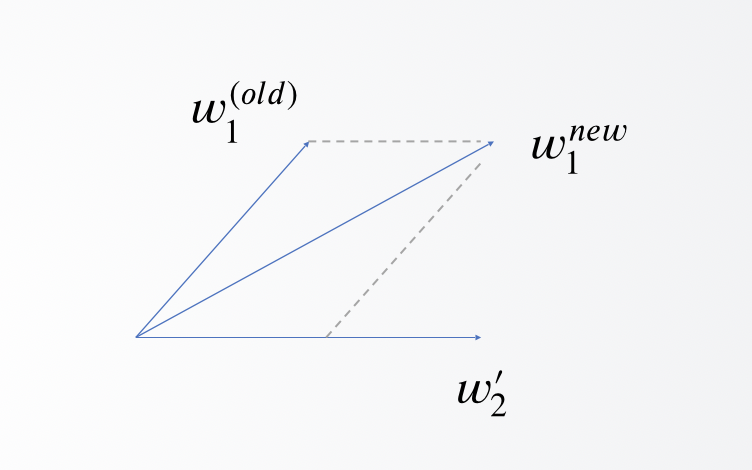
由于只有$e_2$是负数,因此,$w_1$加上了$w^{‘}_2$的分量,从空间上看,两者相互靠近了!
即: $w{知识}$ 靠近了 $w^{‘}{改变}$ ;其余词语的词向量则远离了 $w^{‘}_{改变}$ 。
同理,对于样本「高考 改变 命运」,当我们使用「高考」去预测「改变」时,我们也会发现, $w{高考}$ 向 $w^{‘}{改变}$ 靠近。这样以来, $w_{知识}$ 和 $w{高考}$ 也在互相靠近!
因此,使用word2vec训练词向量,其过程就是相同上下文的词语的词向量相互靠近,不同上下文的词语的词向量相互远离的过程。对于类似上下文的词语,其词向量在空间上更加靠近,向量之间的距离也更短。
4.2 对词向量维度的理解
有了前面的理解,再来看一下词向量的维度。图五中,我们画出了二维向量相互靠近的过程,在二维空间,如果我们想要靠近一个向量,势必也要远离另外一些向量。但如果我们的相似词语比较多时,势必无法靠近所有相似词语的向量。而维度越高,越可以在保持与当前相似向量距离变化不大的情况下,靠近另外一个相似向量。
因此,词向量的维度越高,一个词语能够与越多的词语产生正确的「靠近运动」,表现在语言层面,可以理解为具有更加丰富的语义。一般,训练词向量使用的语料库越大,就应该使用越大的词向量维度,这样也能够得到具备更加丰富语义的词向量。
但词向量的维度并非越高越好,维度越高,词向量所占的存储空间越大,顶层任务所需要的计算量越大。因此,实际使用中,可以根据具体语料库的大小和实际计算要求选择。
5. 不足与改进空间
总的来说,word2vec通过词语与上下文的相互关系来将语义建模到向量中,但word2vec没有考虑词语之间的顺序关系,也没有考虑整个语料库的统计信息(word2vec属于基于预测的词嵌入方法),通过上下文关系建模语义的过程,也会损失许多语义和句法等信息。这就给后续的研究留下了许多可开展的空间……
6. 参考资料推荐
我在学习word2vec的过程中,阅读了非常多的资料,有些对理解Word2Vec帮助巨大,下面我将个人觉得最好的资料推荐出来(百度一下或google一下都能搜到):
【1】word2vec Parameter Learning Explained. Xin Rong ronxin@umich.edu
这篇论文强烈推荐!论文对Word2Vec的四个主要概念进行了非常详细的介绍,也有一些Intutive的解释帮助理解!首推!
【2】Word2Vec中的数学原理详解
强烈推荐!文章介绍Word2Vec的由来和前置知识,最难得的是,文章对四个主要概念都进行了前向传播和反向传播的推导,认真啃下来,对理解Word2Vec帮助巨大!
【3】[NLP] 秒懂词向量Word2vec的本质
我接触Word2Vec前期看的文章,帮助我建立了对Word2Vec的初步认识,理解了Word2Vec到底为何方神圣;文中推荐的许多资料也让我在后续的学习过程中受益匪浅!
tensorflow官方的word2vec基础代码实现,对于理解word2vec的样本构造,训练细节等大有帮助。
